Leetcode刷题 - KMP算法 - Lisheng Xie

KMP算法是一种高效的字符串匹配算法，但是之前每次学过之后都会忘记，这次做一下总结加深印象，主要参考了以下链接。

https://programmercarl.com/0028.%E5%AE%9E%E7%8E%B0strStr.html

问题

给定一个字符串$s$(长度为N)和一个模式串$t$(长度为M)，如果$s$中存在$t$，那么返回模式串第一次出现的起始索引；如果不存在返回-1。对应Leetcode 28. 找出字符串中第一个匹配项的下标

KMP算法

KMP算法是由D.E.Knuth，J.H.Morris和V.R.Pratt同时发现的一种快速的字符串匹配算法，时间复杂度为$O(M+N)$。KMP算法的核心思想是在字符串匹配失败时利用之前已经匹配的信息来做快速回退，避免从头再做匹配。KMP算法的核心函数是一个用于求解next数组的函数，next数组包含了模式串局部匹配的信息。

这里代码随想录中给出了关于next数组的详细解释。next数组对应自定义的前缀表，其中前缀表是一个和模式串长度相同的数组，前缀表第i个位置的值为[0,i]子字符串的最长相同前后缀的长度；

前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串；
举例来说，“aab”的前缀有“a”和“aa”、后缀有“b”和“ab”，“aabaa”的最长相同前后缀长度为2，“aa”的最长相同前后缀长度为1。

以下图为例，假设文本串和模式串分别为aabaabaafa和aabaaf，前缀表如图中所示。那么在b和f不匹配时，此时寻找前缀表中前一位存储的值，查找得到值为2，该值的含义是“aabaa”的最长相同前后缀长度为2，即“aa”。此时我们可以不用从头开始重新匹配，文本串中的匹配指针可以不移动，将模式串中的匹配指针回退到索引2处重新开始匹配即可。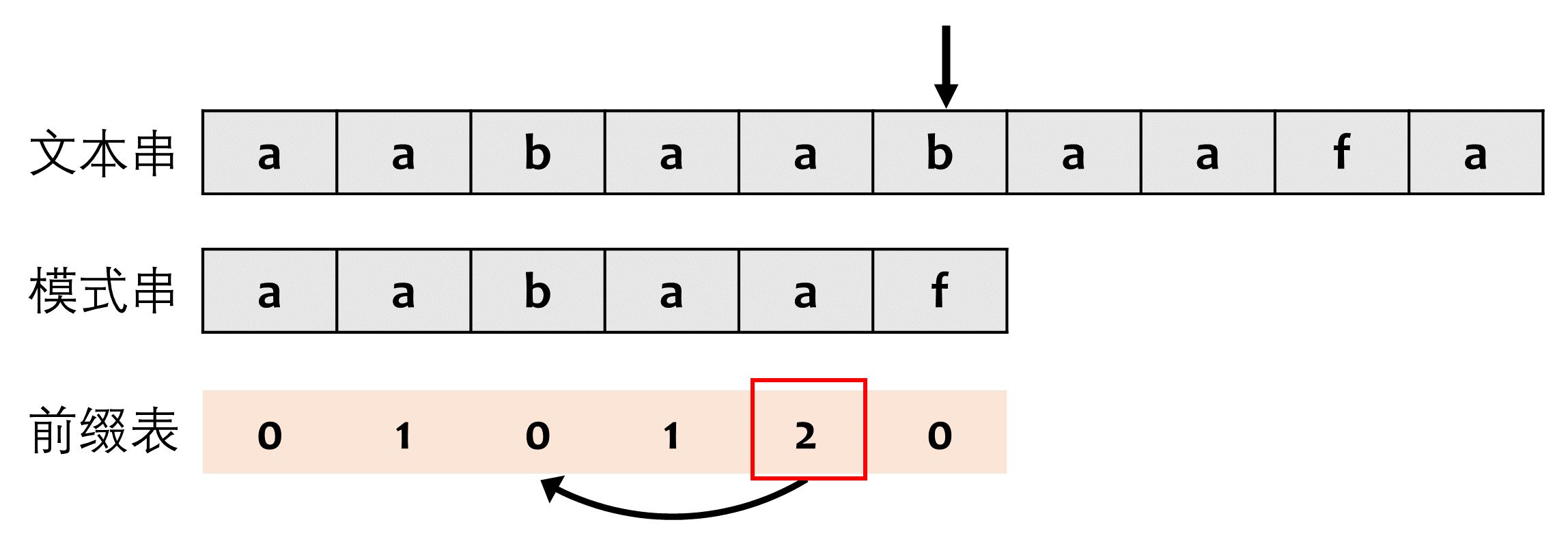
prefix table

这里为什么可以不回退文本串的匹配指针？
因为这里通过回退j指针，找到了从文本串中该位置向前的最长相同前后缀，获得了类似下图的效果。

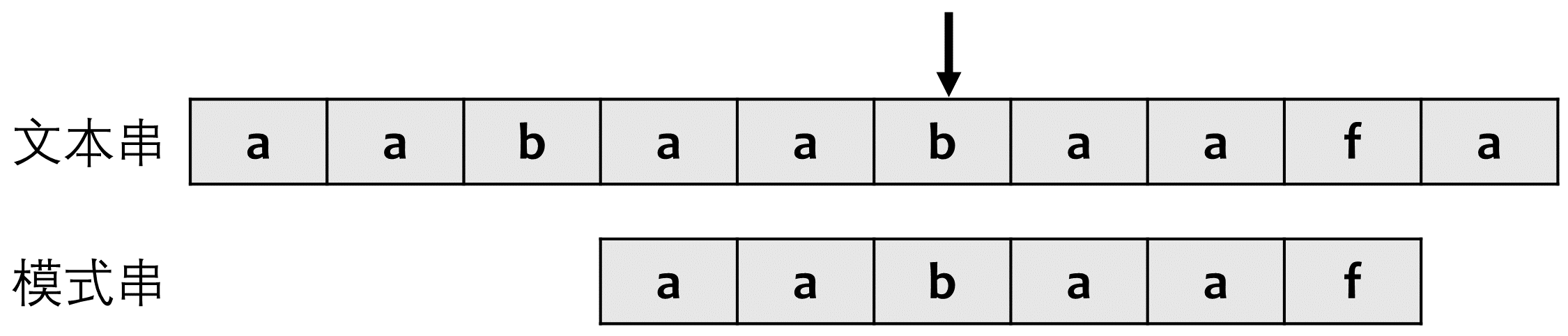
prefix table

实际使用中常通过将前缀表统一减1得到next数组，那么如何计算next数组？

next数组的计算类似于移动模式串，在模式串和模式串之间做匹配，在移动的过程中计算next数组的值，next数组的计算代码如下所示：

void getNext(int* next, const string& s){
  int j = -1;
  next[0] = j;
  for(int i = 1; i < s.size(); i++) { // 注意i从1开始
      while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
          j = next[j]; // 向前回退
      }
      if (s[i] == s[j + 1]) { // 找到相同的前后缀
          j++;
      }
      next[i] = j; // 将j（前缀的长度）赋给next[i]
  }
}

基于next数组进行文本串和模式串的匹配代码如下：

void match(string s, string t) {
  int j = -1;
  int next[t.size()];
  getNext(next, t);

  for (int i = 0; i < s.size(); i++) {
      while (j >= 0 && s[i] != t[j+1]) {
          j = next[j];
      }
      if (s[i] == s[j+1]) {
          j++;
      }
      if (j == (t.size() - 1)) {
        return i - t.size() + 1;
      }
  }
  return -1;
}

Leetcode刷题 - KMP算法

问题

KMP算法

评论 (0)