多目标优化问题
多目标优化(也称为多目标规划、向量优化、多标准优化、多属性优化或帕累托优化)是多标准决策制定的一个领域,涉及同时优化多个目标函数的数学优化问题,需要在权衡取舍的情况下在两个或多个相互冲突的目标之间做出最佳决策。(维基百科)
多目标优化问题中目标函数之间通常相互冲突,求解多目标优化问题通常希望找到可以很好地平衡不同优化目标的解,即帕累托最优解。
多目标优化问题的数学描述
$$\min_{x\in X} (f_1(x),f_2(x),\dots,f_k(x))$$
其中$ k\geq 2 $,$ (f_1(x),f_2(x),\dots,f_k(x)) $式决策函数集合。
帕累托最优
帕累托最优是指这样一种情况,没有可用的行动或分配可以使一个人过得更好而不会使另一个人过得更糟。多目标优化问题中我们希望找到的就是帕累托最优解,再由决策者决定具体使用那个解。帕累托最优解集指的是所有可行解中的不可支配解集,下面我们将介绍支配和不可支配解集的概念。
支配和不可支配解集
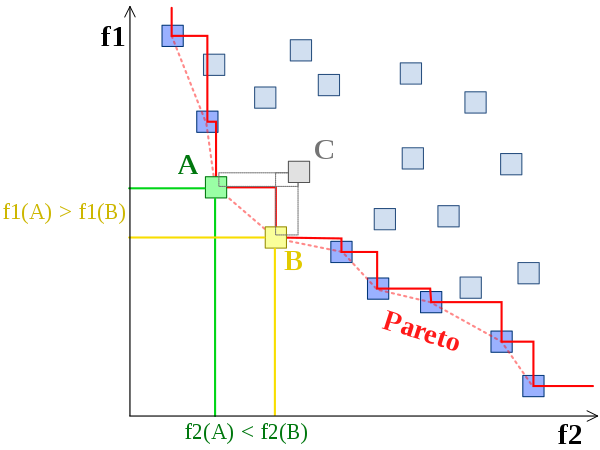
当解$ x_1 $和$ x_2 $满足以下两个条件时
* 对于所有的目标函数,$ f_i(x_1)\leq f_i(x_2) $,其中$ 1\leq i \leq k $
* 至少由一个目标函数$ f_i(x) $满足$ f_i(x_1) < f_i(x_2) $,其中$ 1\leq i \leq k $
我们称$ x_1 $支配$ x_2 $,如上图中$ A $和$ B $都支配$ C $,但彼此之间不存在支配关系。
当一个解集中任何一个解都不能被该集合中其他解支配,那么就称该解集为不可支配解集。一组帕累托最优结果,如上图中红色的边界,称为帕累托前沿或帕累托边界。
求解多目标优化问题的方法主要分为两类,一种是将多目标优化问题转换成单目标优化问题,常用的方法是对目标函数值加权求和或保留一个目标函数、其余的目标函数被转化为限定条件。但是由于实际应用中目标函数的函数值范围不好确定,因此转换成单目标优化算法的效果常常不好。实际应用更加广泛的是另一种采用多目标的优化算法。
多目标粒子群算法MOPSO
多目标粒子群算法最早由Coello等人提出[1],算法的大致处理步骤如下所示:
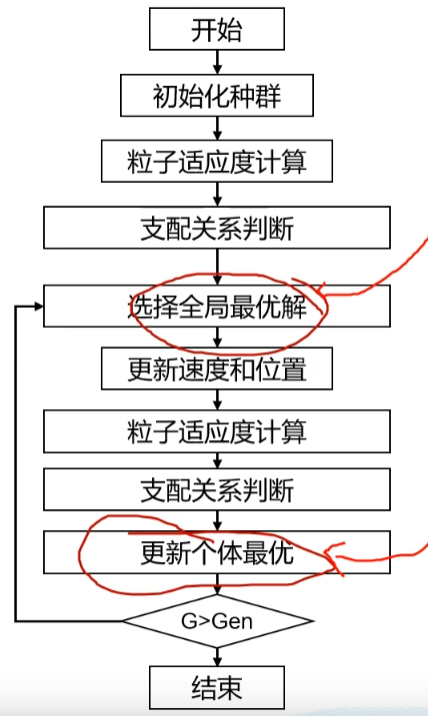
和粒子群算法不同的是,这里添加了支配关系判断的步骤,同时选择全局最优解以及更新个体最优的步骤和粒子群算法也有所不同。此外,MOPSO还额外维护了精英解和解空间的网格,下面我们将分别加以介绍。
首先是支配关系的判断,根据第一部分中对于帕累托前沿和支配关系的介绍,我们知道多目标优化问题中解的优劣由支配关系来加以判断。
每次迭代开始时,我们需要从精英解集合中选择当前的全局最优解,精英解中包含的是不被其他解支配的解的集合,换言之,精英解包含的是目前获取到的帕累托前沿。选择全局最优解的步骤如下:
1. 在解集空间中绘制网格,即根据当前的解集中不同目标函数的最大值和最小值,将空间均匀等分并给每个子空间添加索引,确定不同的解所对应的子空间。
2. 对于包含解的子空间,判断每个子空间中存在的解个数$ N_1,\cdots,N_k $,使用轮盘赌算法获取当前的全局最优解,轮盘赌的概率和解的个数呈反相关关系(让解稀疏的子空间拥有更大的被选中的概率,设法让解在帕累托前沿上分布更均匀)。
选择好当前的全局最优解后更新粒子的位置和速度,更新公式和粒子群算法一致。
$$v_i = w \times v_i + c_1\times rand() \times ((p_{best})_i-x_i) + c_2\times rand()\times ((g_{best})_i-x_i)$$
粒子更新后会根据粒子当前解和局部最优解之间的支配关系更新粒子的局部最优解。在更新局部最优解之前,还可以采取类似于遗传算法的步骤,以一定的概率对粒子的当前解进行变异。
更新完局部最优解之后更新精英解集合,保留当前不被其他解支配的解,同时为了避免精英解过大,可以设置一个阈值来控制精英解集合中的解数目,多余的精英解被随机抛弃。
多目标遗传算法NSGA-II
多目标遗传算法NSGA-II由Deb等人提出[2],算法的大致处理步骤如下所示:
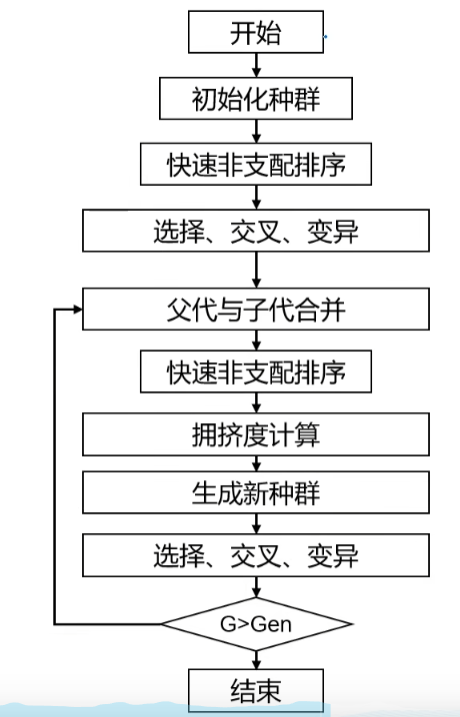
相较于单目标进化算法添加了快速非支配排序和父代、子代合并操作增加种群多样性,此外从$ rank_i $ 中取出一部分个体有两种方式、一种是拥挤距离排序、另一种是随机选择。下面我们将分别加以介绍。
对于当前已有的父代解和子代集合,融合两个集合产生当前的解集合,首先执行非支配排序,非支配排序的大致步骤为,先找出解集中的非支配边沿,将这部分的解的$ rank $置为1;去掉这部分解,继续找出剩下的解集中的非支配边沿,将这部分的解的$ rank $置为2,重复上述步骤知道遍历完所有的解。实际实现中需要记录每个解支配的解,方便后续的$ rank $计算,具体可以参考后面的参考代码实现。
在当前解集合中选取下一轮迭代的父代解集合。需要注意的是对于固定大小的父代解集合,这里依次从$ rank=1 $的解开始加入,知道数量满足要求。最后可能需要从$ rank=i $的解集合中选取一部分,此时有两种方式,一种是随机选取,一种是根据拥挤度距离排序后选取。拥挤度距离计算的示意图如下,
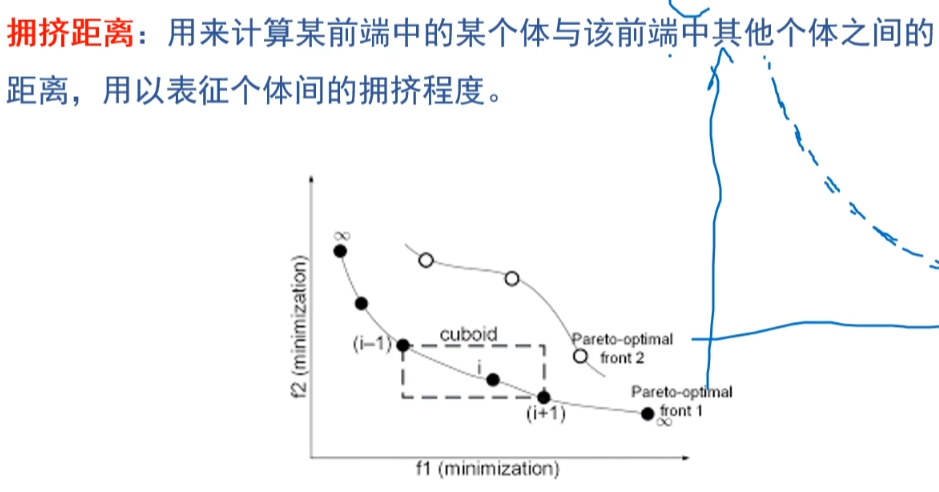
拥挤度距离可以用来衡量当前解周围的解的密度,优先选择拥挤度距离大(解稀疏)的地方可以使得最后求得的帕累托前沿上解分布更均匀。
对当前的解执行交叉变异操作产生下一轮迭代的子代解,交叉变异操作可以有不同的实现。
代码实现
目标函数
# -*- coding : utf-8 -*-
from collections import defaultdict
import math
import numpy as np
def ZDT1(x):
"""
测试函数——ZDT1
:parameter
:param x: 为 m 维向量,表示个体的具体解向量
:return f: 为两个目标方向上的函数值
"""
poplength = len(x)
f = defaultdict(float)
g = 1 + 9 * sum(x[1:poplength]) / (poplength - 1)
f[1] = x[0]
f[2] = g * (1 - pow(x[0] / g, 0.5))
return f
def ZDT2(x):
poplength = len(x)
f = defaultdict(float)
g = 1 + 9 * sum(x[1:poplength]) / (poplength - 1)
f[1] = x[0]
f[2] = g * (1 - (x[0] / g) ** 2)
return f
def KUR(x):
f = defaultdict(float)
poplength = len(x)
f[1] = 0
for i in range(poplength - 1):
f[1] = f[1] + (-10) * math.exp((-0.2) * (x[i] ** 2 + x[i+1] ** 2) ** 0.5)
for i in range(poplength):
f[2] = abs(x[i]) ** 0.8 + 5 * math.sin(x[i] ** 3)
return f
# 轮盘赌函数
def RouletteWheelSelection(P):
idx = np.argsort(P)
val = np.sort(P)
prob = [_/sum(P) for _ in val] # 概率
dprob = np.cumsum(prob) # 累积概率
seed = np.random.random() # 随机数
res = idx[(dprob>seed).tolist().index(True)] # 选择
return res
MOPSO
参考了Matlab实现
# -*- coding: utf-8 -*-
# Lishengxie
# 2023-03-03
# Implementation of multi-objective particle swarm algorithm
from collections import defaultdict
import numpy as np
from utils import ZDT1, ZDT2, KUR, RouletteWheelSelection
import matplotlib.pyplot as plt
import copy
class Particle:
"""
Implementation of particle class, which provides the constraints for particle's position and the method to compute dominance.
"""
def __init__(self):
self.position = None
self.velocity = None
self.best = None
self.cost = defaultdict()
self.is_dominated = False
def bound_position(self, var_min, var_max):
"""
对解向量 solution 中的每个分量进行定义域判断,超过最大值,将其赋值为最大值;小于最小值,赋值为最小值
Args:
var_min: 位置域下限
var_max: 位置域上限
Returns:
None
"""
self.position = np.clip(self.position, var_min, var_max)
def update_position(self, var_min, var_max):
"""
Update particle'sposition
Args:
var_min: 位置域下限
var_max: 位置域上限
Returns:
None
"""
self.position += self.velocity
self.bound_position(var_min, var_max)
def cal_cost(self, objective_func):
"""
Calculate the objective scores.
Args:
objective_func: Function, return objective scores with position given.
Return:
cost: collection.defaultdict, cost function scores with keys from `1` to `N`.
"""
return objective_func(self.position)
def dominate(self, other):
"""
Return the dominance relationship between the current particle and input particle. `A` dominates `B` if any of `A`'s cost is less than or equal to `B` and at least one of `A`'s cost is less than `B`.
Args:
other: Particle, the other particle to be compared
"""
v1 = np.array(list(self.cost.values()))
v2 = np.array(list(other.cost.values()))
return (v1<=v2).all() and (v1<v2).any()
class MOPSO:
"""
Multi-objective particle swarm optimization algorithm.
"""
def __init__(self, max_iter=200, n_pop=200, n_rep=100,\
w=0.5, wdamp=0.99, c1=1., c2=2., n_grid=7, alpha=0.1,\
beta=2., gamma=2., mu=0.1, n_var=5, var_min=0., var_max=1., \
objective_func=ZDT1, objective_num=2):
"""
Args:
max_iter: int, Maximum Number of Iterations
n_pop: int, Population Size
n_rep: int, Repository Size
w: float, Intertia Weight
wdamp: float, Intertia Weight Damping Rate
c1: float, Personal Learning Coefficient
c2: float, Global Learning Coefficient
n_grid: int, number of Grids per Dimension
alpha: float, Inflation Rate
beta: float, Leader Selection Pressure
gamma: float, Deletion Selection Pressure
mu: float, Mutation Rate
n_var: int, Number of decision variables
var_max: float, Lower Bound of Variables
var_min: float, Upper Bound of Variables
objective_func: function, cost function to minimize
objective_num: int, number of cost function
Returns:
None
"""
self.max_iter = max_iter
self.n_pop = n_pop
self.n_rep = n_rep
self.w = w
self.wdamp = wdamp
self.c1 = c1
self.c2 = c2
self.n_grid = n_grid
self.alpha = alpha
self.beta = beta
self.gamma = gamma
self.mu = mu
self.n_var = n_var
self.var_max = var_max
self.var_min = var_min
self.objective_func = objective_func
self.objective_num = objective_num
# particle swam
self.particles = []
# repository, which stores the dominant particles on the Pareto Front
self.repository = []
# init particle swam
self.init_particle()
# grid matrix, avoiding the computation of crowding distance
self.grid = np.zeros((self.objective_num, self.n_grid + 2))
self.grid_index = None
self.grid_subindex = None
def init_particle(self):
"""
Init particles with the number of `n_pop`
"""
for i in range(self.n_pop):
# init a particle
p = Particle()
p.position = np.random.random(self.n_var) * (self.var_max-self.var_min) + self.var_min
p.velocity = np.zeros(self.n_var)
# cost dict
p.cost = p.cal_cost(self.objective_func)
# local best solution
p.best = Particle()
p.best.position = p.position
p.best.cost = p.cost
# add particle to the particle swam
self.particles.append(p)
def determine_domination(self, pop):
"""
Determine the dominance relationship in a given group of particles.
Args:
pop: List[Particle], group of particles
"""
n_pop = len(pop)
# reset all the `is_dominated` be False
for i in range(n_pop):
pop[i].is_dominated = False
# traverse all of the particle pairs
for i in range(n_pop-1):
for j in range(i+1, n_pop):
if pop[i].dominate(pop[j]):
pop[j].is_dominated = True
if pop[j].dominate(pop[i]):
pop[i].is_dominated = True
return pop
def determine_repository(self, pop):
"""
Add the particle `p` in `pop` to `repository` if `p` is not been dominated.
Args:
pop: List[Particle], group of particles
"""
for i in range(len(pop)):
if not pop[i].is_dominated:
self.repository.append(copy.deepcopy(pop[i]))
def create_grid(self, pop):
"""
Create grids in cost function space(2D or more), limited by the maximum and minimum value of cost funciton.
Args:
pop: List[Particle], group of particles
"""
n_pop = len(pop)
cost = np.zeros((self.objective_num, n_pop))
# Get cost of each particle
for c in range(1, self.objective_num+1):
for i in range(n_pop):
cost[c-1][i] = pop[i].cost[c]
cmin = np.min(cost, axis=1)
cmax = np.max(cost, axis=1)
dc = cmax-cmin
cmin = cmin - self.alpha * dc;
cmax = cmax + self.alpha * dc;
for j in range(self.objective_num):
self.grid[j] = np.append(np.linspace(cmin[j], cmax[j], self.n_grid+1), np.inf)
return cost
def find_grid_index(self, pop, cost):
"""
Find the grid index for each particle in the grids matrix, the multi-dimensional index is transfered to integer.
Args:
pop: List[Particle], group of particles
cost: numpy.ndarray, cost function matrix for particles in `pop`.
"""
n_pop = len(pop)
self.grid_subindex = np.zeros((n_pop, self.objective_num), dtype=np.uint)
self.grid_index = np.zeros((n_pop), dtype=np.uint)
for i in range(n_pop):
for j in range(self.objective_num):
self.grid_subindex[i][j] = np.argwhere(self.grid[j] > cost[j][i])[0]
if j == 0:
self.grid_index[i] = self.grid_subindex[i][j]
else:
self.grid_index[i] = (self.grid_index[i]-1)*self.n_grid + self.grid_subindex[i][j]
def select_leader(self):
"""
Select a leader from `repository` based on the Roulette algorithm. More about the Roulette algorithm, refer to `https://blog.csdn.net/doubi1/article/details/115923275`
"""
# occupied cells
oc = np.unique(self.grid_index)
# number of particles in the occupied cells
N = np.zeros_like(oc)
for i in range(len(N)):
N[i] = np.sum(self.grid_index==oc[i])
P = np.exp(-self.beta*N)
P = P/np.sum(P)
sel = RouletteWheelSelection(P)
# selected cell
sc = oc[sel]
# selected cell members
scm = np.argwhere(self.grid_index==sc).flatten()
# selected member
sm = scm[np.random.randint(0, len(scm))]
return self.repository[sm]
def mutate(self, position, pm):
"""
Select a particle `j`(randomly selected) to conduct mutation.
Args:
pm: float, mutation scale.
"""
j = np.random.randint(0, self.n_var)
dx = pm * (self.var_max - self.var_min)
lb = position[j] - dx
if lb < self.var_min:
lb = self.var_min
ub = position[j] + dx
if ub > self.var_max:
ub = self.var_max
x_new = position
x_new[j] = np.random.random() * (ub-lb) + lb
return x_new
def delete_one_rep_member(self):
"""
Select a particle from `repository` and delete it.
"""
# occupied cells
oc = np.unique(self.grid_index)
# number of particles in the occupied cells
N = np.zeros_like(oc)
for i in range(len(N)):
N[i] = np.sum(self.grid_index==oc[i])
P = np.exp(self.gamma*N)
P = P/np.sum(P)
sel = RouletteWheelSelection(P)
# selected cell
sc = oc[sel]
# selected cell members
scm = np.argwhere(self.grid_index==sc).flatten()
# selected member
sm = scm[np.random.randint(0, len(scm))]
self.repository[sm] = None
def plot(self):
X = []
Y = []
X2 = []
Y2 = []
for ind in self.particles:
X.append(ind.cost[1])
Y.append(ind.cost[2])
for ind in self.repository:
X2.append(ind.cost[1])
Y2.append(ind.cost[2])
# plt.xlim(0, 1)
# plt.ylim(0, 1)
plt.xlabel('F1')
plt.ylabel('F2')
plt.scatter(X, Y)
plt.scatter(X2, Y2)
def solve(self):
"""
Execute the optimization process.
"""
# Init step
self.particles = self.determine_domination(self.particles)
self.determine_repository(self.particles)
cost = self.create_grid(self.repository)
self.find_grid_index(self.repository, cost)
# Main loop
for it in range(self.max_iter):
for i in range(self.n_pop):
# select the global best particle
leader = self.select_leader()
# update particle's velocity and position
self.particles[i].velocity = self.w * self.particles[i].velocity \
+ self.c1 * np.random.random(self.n_var) * (self.particles[i].best.position - self.particles[i].position) \
+ self.c2 * np.random.random(self.n_var) * (leader.position - self.particles[i].position)
self.particles[i].update_position(self.var_min, self.var_max)
self.particles[i].cost = self.particles[i].cal_cost(self.objective_func)
# Apply Mutation
pm = (1-(it-1) / (self.max_iter - 1)) ** (1./self.mu)
if np.random.random() < pm:
new_sol = Particle()
new_sol.position = self.mutate(self.particles[i].position, pm)
new_sol.cost = new_sol.cal_cost(self.objective_func)
if new_sol.dominate(self.particles[i]):
self.particles[i].position = new_sol.position
self.particles[i].cost = new_sol.cost
elif self.particles[i].dominate(new_sol):
pass
else:
if np.random.random() < 0.5:
self.particles[i].position = new_sol.position
self.particles[i].cost = new_sol.cost
# update locate best solution
if self.particles[i].dominate(self.particles[i].best):
self.particles[i].best.position = self.particles[i].position
self.particles[i].best.cost = self.particles[i].cost
elif self.particles[i].best.dominate(self.particles[i]):
pass
else:
if np.random.random() < 0.5:
self.particles[i].best.position = self.particles[i].position
self.particles[i].best.cost = self.particles[i].cost
# update `repository`
# for each in self.particles:
# self.repository.append(each)
self.determine_repository(self.particles)
self.repository = self.determine_domination(self.repository)
tmp = []
for each in self.repository:
if not each.is_dominated:
tmp.append(each)
self.repository = tmp
# update cost grid based on `repository`
cost = self.create_grid(self.repository)
self.find_grid_index(self.repository, cost)
# delete particles randomly from `repository` which is out of capacity
if len(self.repository) > self.n_rep:
for _ in range(len(self.repository) - self.n_rep):
self.delete_one_rep_member()
# update grid index for the next loop
grid_index = []
repository = []
for i in range(len(self.repository)):
if self.repository[i] is None:
continue
else:
grid_index.append(self.grid_index[i])
repository.append(self.repository[i])
self.grid_index = grid_index
self.repository = repository
plt.clf()
plt.title('current iteration:' + str(it + 1))
self.plot()
plt.pause(0.01)
print("Iteration {}: number of rep members = {}".format(it, len(self.repository)))
self.w = self.w * self.wdamp
plt.show()
if __name__ == "__main__":
# mopso = MOPSO(objective_func=KUR, var_max=5, var_min=-5, n_var=3, max_iter=400, n_pop=100)
mopso = MOPSO(objective_func=ZDT1)
mopso.solve()
NSGA-II
参考了开源实现
# -*- coding = utf-8 -*-
from collections import defaultdict
import numpy as np
import random
import matplotlib.pyplot as plt
import math
from utils import ZDT1, ZDT2, KUR
class Individual(object):
def __init__(self):
self.solution = None # 实际赋值中是一个 nparray 类型,方便进行四则运算
self.objective = defaultdict()
self.n = 0 # 解p被几个解所支配,是一个数值(左下部分点的个数)
self.rank = 0 # 解所在第几层
self.S = [] # 解p支配哪些解,是一个解集合(右上部分点的内容)
self.distance = 0 # 拥挤度距离
def bound_process(self, bound_min, bound_max):
"""
对解向量 solution 中的每个分量进行定义域判断,超过最大值,将其赋值为最大值;小于最小值,赋值为最小值
:param bound_min: 定义域下限
:param bound_max: 定义域上限
:return:
"""
for i, item in enumerate(self.solution):
if item > bound_max:
self.solution[i] = bound_max
elif item < bound_min:
self.solution[i] = bound_min
def calculate_objective(self, objective_fun):
self.objective = objective_fun(self.solution)
# 重载小于号“<”
def __lt__(self, other):
v1 = list(self.objective.values())
v2 = list(other.objective.values())
for i in range(len(v1)):
if v1[i] > v2[i]:
return 0 # 但凡有一个位置是 v1大于v2的 直接返回0,如果相等的话比较下一个目标值
return 1
# 重载大于号“>”
def __gt__(self, other):
v1 = list(self.objective.values())
v2 = list(other.objective.values())
for i in range(len(v1)):
if v1[i] < v2[i]:
return 0 # 但凡有一个位置是 v1小于v2的 直接返回0
return 1
class NSGAII:
def __init__(self, max_iter=200, n_pop=100, n_var=30,\
eta=1, var_min=0, var_max=1, objective_fun = ZDT1):
"""
Args:
max_iter: int, Maximum Number of Iterations
n_pop: int, Population Size
eta: float, 变异分布参数,该值越大则产生的后代个体逼近父代的概率越大;Deb建议设为 1
n_var: int, Number of decision variables
var_max: float, Lower Bound of Variables
var_min: float, Upper Bound of Variables
objective_func: function, cost function to minimize
Returns:
None
"""
self.max_iter = max_iter
self.n_pop = n_pop
self.n_var = n_var
self.eta = eta
self.var_min = var_min
self.var_max = var_max
self.objective_fun = objective_fun
self.P = []
self.init_P()
def init_P(self):
for i in range(self.n_pop):
self.P.append(Individual())
# 随机生成个体可行解
self.P[i].solution = np.random.rand(self.n_var) * (self.var_max - self.var_min) + self.var_min
self.P[i].bound_process(self.var_min, self.var_max) # 定义域越界处理
self.P[i].calculate_objective(self.objective_fun) # 计算目标函数值
def fast_non_dominated_sort(self, P):
"""
非支配排序
:param P: 种群 P
:return F: F=(F_1, F_2, ...) 将种群 P 分为了不同的层, 返回值类型是dict,键为层号,值为 List 类型,存放着该层的个体
"""
F = defaultdict(list)
for p in P:
p.S = []
p.n = 0
for q in P:
if p < q: # if p dominate q
p.S.append(q) # Add q to the set of solutions dominated by p
elif q < p:
p.n += 1 # Increment the domination counter of p
if p.n == 0:
p.rank = 1
F[1].append(p)
i = 1
while F[i]:
Q = []
for p in F[i]:
for q in p.S:
q.n = q.n - 1
if q.n == 0:
q.rank = i + 1
Q.append(q)
i = i + 1
F[i] = Q
return F
def crowding_distance_assignment(self, L):
""" 传进来的参数应该是L = F(i), 类型是List"""
l = len(L) # number of solution in
for i in range(l):
L[i].distance = 0 # initialize distance
for m in L[0].objective.keys():
L.sort(key=lambda x: x.objective[m]) # sort using each objective value
L[0].distance = float('inf')
L[l - 1].distance = float('inf') # so that boundary points are always selected
# 排序是由小到大的,所以最大值和最小值分别是 L[l-1] 和 L[0]
f_max = L[l - 1].objective[m]
f_min = L[0].objective[m]
for i in range(1, l - 1): # for all other points
L[i].distance = L[i].distance + (L[i + 1].objective[m] - L[i - 1].objective[m]) / (f_max - f_min)
# 虽然发生概率较小,但为了防止除0错,当bug发生时请替换为以下代码
# if f_max != f_min:
# for i in range(1, l - 1): # for all other points
# L[i].distance = L[i].distance + (L[i + 1].objective[m] - L[i - 1].objective[m]) / (f_max - f_min)
def binary_tournament(self, ind1, ind2):
"""
二元锦标赛
:param ind1:个体1号
:param ind2: 个体2号
:return:返回较优的个体
"""
if ind1.rank != ind2.rank: # 如果两个个体有支配关系,即在两个不同的rank中,选择rank小的
return ind1 if ind1.rank < ind2.rank else ind2
elif ind1.distance != ind2.distance: # 如果两个个体rank相同,比较拥挤度距离,选择拥挤读距离大的
return ind1 if ind1.distance > ind2.distance else ind2
else: # 如果rank和拥挤度都相同,返回任意一个都可以
return ind1
def make_new_pop(self, P, eta, bound_min, bound_max, objective_fun):
"""
use select,crossover and mutation to create a new population Q
:param P: 父代种群
:param eta: 变异分布参数,该值越大则产生的后代个体逼近父代的概率越大。Deb建议设为 1
:param bound_min: 定义域下限
:param bound_max: 定义域上限
:param objective_fun: 目标函数
:return Q : 子代种群
"""
popnum = len(P)
Q = []
# binary tournament selection
for i in range(int(popnum / 2)):
# 从种群中随机选择两个个体,进行二元锦标赛,选择出一个 parent1
i = random.randint(0, popnum - 1)
j = random.randint(0, popnum - 1)
parent1 = self.binary_tournament(P[i], P[j])
# 从种群中随机选择两个个体,进行二元锦标赛,选择出一个 parent2
i = random.randint(0, popnum - 1)
j = random.randint(0, popnum - 1)
parent2 = self.binary_tournament(P[i], P[j])
while (parent1.solution == parent2.solution).all(): # 如果选择到的两个父代完全一样,则重选另一个
i = random.randint(0, popnum - 1)
j = random.randint(0, popnum - 1)
parent2 = self.binary_tournament(P[i], P[j])
# parent1 和 parent1 进行交叉,变异 产生 2 个子代
Two_offspring = self.crossover_mutation(parent1, parent2, eta, bound_min, bound_max, objective_fun)
# 产生的子代进入子代种群
Q.append(Two_offspring[0])
Q.append(Two_offspring[1])
return Q
def crossover_mutation(self, parent1, parent2, eta, bound_min, bound_max, objective_fun):
"""
交叉方式使用二进制交叉算子(SBX), 变异方式采用多项式变异(PM)
:param parent1: 父代1
:param parent2: 父代2
:param eta: 变异分布参数, 该值越大则产生的后代个体逼近父代的概率越大。Deb建议设为 1
:param bound_min: 定义域下限
:param bound_max: 定义域上限
:param objective_fun: 目标函数
:return: 2 个子代
"""
poplength = len(parent1.solution)
offspring1 = Individual()
offspring2 = Individual()
offspring1.solution = np.empty(poplength)
offspring2.solution = np.empty(poplength)
# 二进制交叉
for i in range(poplength):
rand = random.random()
beta = (rand * 2) ** (1 / (eta + 1)) if rand < 0.5 else (1 / (2 * (1 - rand))) ** (1.0 / (eta + 1))
offspring1.solution[i] = 0.5 * ((1 + beta) * parent1.solution[i] + (1 - beta) * parent2.solution[i])
offspring2.solution[i] = 0.5 * ((1 - beta) * parent1.solution[i] + (1 + beta) * parent2.solution[i])
# 多项式变异
# TODO 变异的时候只变异一个,不要两个都变,不然要么出现早熟现象,要么收敛速度巨慢 why?
for i in range(poplength):
mu = random.random()
delta = 2 * mu ** (1 / (eta + 1)) if mu < 0.5 else (1 - (2 * (1 - mu)) ** (1 / (eta + 1)))
offspring1.solution[i] = offspring1.solution[i] + delta
# 定义域越界处理
offspring1.bound_process(bound_min, bound_max)
offspring2.bound_process(bound_min, bound_max)
# 计算目标函数值
offspring1.calculate_objective(objective_fun)
offspring2.calculate_objective(objective_fun)
return [offspring1, offspring2]
def solve(self):
# 否 -> 非支配排序
self.fast_non_dominated_sort(self.P)
Q = self.make_new_pop(self.P, self.eta, self.var_min, self.var_max, self.objective_fun)
P_t = self.P # 当前这一届的父代种群
Q_t = Q # 当前这一届的子代种群
for gen_cur in range(self.max_iter):
R_t = P_t + Q_t # combine parent and offspring population
F = self.fast_non_dominated_sort(R_t)
P_n = [] # 即为P_t+1,表示下一届的父代
i = 1
while len(P_n) + len(F[i]) < self.n_pop: # until the parent population is filled
self.crowding_distance_assignment(F[i]) # calculate crowding-distance in F_i
P_n = P_n + F[i] # include ith non dominated front in the parent pop
i = i + 1 # check the next front for inclusion
F[i].sort(key=lambda x: x.distance) # sort in descending order using <n,因为本身就在同一层,所以相当于直接比拥挤距离
P_n = P_n + F[i][:self.n_pop - len(P_n)]
Q_n = self.make_new_pop(P_n, self.eta, self.var_min, self.var_max,
self.objective_fun) # use selection,crossover and mutation to create a new population Q_n
# 求得下一届的父代和子代成为当前届的父代和子代,,进入下一次迭代 《=》 t = t + 1
P_t = P_n
Q_t = Q_n
# 绘图
plt.clf()
plt.title('current generation:' + str(gen_cur + 1))
self.plot_P(P_t)
plt.pause(0.1)
plt.show()
return 0
def plot_P(self, P):
"""
假设目标就俩,给个种群绘图
:param P:
:return:
"""
X = []
Y = []
X1 = []
Y1 = []
for ind in P:
X.append(ind.objective[1])
Y.append(ind.objective[2])
if ind.rank == 1:
X1.append(ind.objective[1])
Y1.append(ind.objective[2])
plt.xlabel('F1')
plt.ylabel('F2')
plt.scatter(X, Y)
plt.scatter(X1, Y1)
def show_some_ind(self, P):
# 测试使用
for i in P:
print(i.solution)
if __name__ == '__main__':
solver = NSGAII()
solver.solve()
参考文献
[1] Coello C A C, Lechuga M S. MOPSO: A proposal for multiple objective particle swarm optimization[C]//Proceedings of the 2002 Congress on Evolutionary Computation. CEC'02 (Cat. No. 02TH8600). IEEE, 2002, 2: 1051-1056.
[2] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE transactions on evolutionary computation, 2002, 6(2): 182-197.

评论 (0)