ziplist

为什么需要 ziplist？

由于 Redis 是一个内存型数据库，因此在使用相应的数据结构时需要1）节省内存空间，2）提高操作效率。传统的包含指向相邻节点指针的双向链表中在内存使用和操作效率上存在一些问题：

1. 存储指针需要额外的内存空间，且该空间在指定硬件平台上是固定的。当存储的数据长度较小时，指针占用空间甚至会超过数据占用空间。
2. 传统双向链表中相邻节点在内存中并不连续，这虽然利用了碎片化的内存空间，但是由于增加了一次额外的指针索引，遍历效率低。

ziplist 是 Redis 中设计的一种内存紧凑型的数据结构，可以用来代替传统的双向链表结构。ziplist 使用一块连续的内存空间，通过在每个节点中存储当前及前一个节点的长度来实现双向遍历，节省内存空间，操作效率高。

ziplist 是什么？

下面给出了压缩列表的结构示意图，包括 10byte 的表头元数据，若干个列表节点以及最后的 1byte 的结束标识符。

| zlbytes | zltail | zllen | entry1 | entry2 | ... | entryN | zlend |

# 各部分说明
zlbytes: 整个压缩列表占用的字节数，uint32_t(4byte)
zltail: 压缩列表表尾节点距离压缩列表的起始地址有多少字节，uint32_t(4byte)
zllen: 压缩列表包含的节点数，uint16_t(2byte)，当该属性值为 UINT16_MAX 时，真实节点数量需要遍历整个压缩列表才能得到
entry: 压缩列表节点
zlend: 用于标记压缩列表末端的特殊值(0xFF)，1byte

每个压缩列表的节点中存储的内容可以看作一个字节数组或者整数值，每个节点包含以下三部分内容：

| previous_entry_length | encoding | content |

# 各部分说明
previous_entry_length: 记录前一个节点的长度，长度为 1byte 或 5byte
    - 前一个节点长度小于 254 字节时，previous_entry_length 长度为 1 字节，记录前一个节点的长度
    - 前一个节点长度大于等于 254 字节时，previous_entry_length 长度为 5 字节，其中第一个字节设置为 0xFE，后面的四个字节用于记录前一个节点长度
encoding: 记录节点的 content 中所保存数据的类型和长度
    - 一字节(00开头)、两字节(01开头)或五字节(10开头)的表示字节数组编码，去除最高两位之后的其他位是字节数组长度
    - 一字节长(11开头)的表示整数编码，去除最高两位后的其他位可以用于标识整数的类型和位宽
content: 节点值，可以是一个字节数组或者整数值，由 encoding 属性决定

ziplist 有什么问题？

前面提到 ziplist 通过使用连续的内存块和精心设计的编码格式来保存列表数据，并实现双向检索的功能。但是，使用 ziplist 仍然存在一些缺点：

1. 遍历复杂度高。ziplist 中记录了尾部节点的偏移，可以快速定位到第一个和最后一个节点，同时通过在每个节点中编码节点本身以及前一个节点的字节数，可以实现前向和后向的遍历。但是，当需要查找中间的元素时，就需要从头部后从尾部遍历，复杂度为 O(n)；
2. 内存重分配。由于 ziplist 使用的是一整块内存，因此在插入或者更新节点时，需要重新结算使用的内存块大小并重新分配内存。特别地，由于节点中存储了前一个节点的长度 previous_entry_length，而该属性是会发生变化的，可能会引发后续的节点依次更新导致 ”连锁更新“ 问题。

针对遍历复杂度高的问题，Redis 在配置文件 redis.conf 中提供了相应参数，用来约束 Hash 和 Zset 结构使用 ziplist 存储时的元素个数以及最大的元素大小，如下所示。例如，在 hash 中元素不超过 512 个，每个元素大小不超过 64byte 时，使用 ziplist 来存储 hash。

hash-max-ziplist-entries 512
hash-max-ziplist-value 64

zset-max-ziplist-entries 128
zset-max-ziplist-value 64

连锁更新

前面我们提到 ziplist 中每个节点中使用 previous_entry_length 保存了前一个节点的长度，当插入、更新或者删除节点时，除了修改节点本身，还需要更新该节点的下一个节点的 previous_entry_length。但是，previous_entry_length 本身并不是定长的，会随着前一个节点的长度发生变化。

考虑下面这种情况，e1 到 eN 的所有节点长度都介于 250 到 253 字节之间，此时 previous_entry_length 只需要使用 1 字节的长度。

| zlbytes | zltail | zllen | e1 | e2 | e3 | ... | eN | zlend | 

此时，我们将一个长度为 254 的新节点设置为压缩列表的头节点，此时 e1 中的 previous_entry_length 需要使用 5 字节存储前一个节点的长度。e1 修改完成后其节点长度大于等于 254 字节，需要进一步修改 e2 节点。e2 节点修改后会出现同样的问题，需要连续修改列表节点直至最后一个 eN 节点。

| zlbytes | zltail | zllen | new | e1 | e2 | e3 | ... | eN | zlend | 

由于更新节点时需要重新分配内存空间，复杂度为 O(N)，而连锁更新最坏情况下可能会引发所有节点的更新，复杂度为 O(N^2)。不过考虑到需要连续多个长度介于 250 到 253 字节的节点才有可能发生连续更新，实际出现的概率很低，但是发生时的更新代价较高。

quicklist

为什么需要 quicklist？

在 Redis 早期版本中，使用压缩列表（ziplist）和双向链表来作为 List 的底层实现。当元素个数较少且元素长度较小时，使用压缩列表作为其底层存储；否则使用双向链表作为底层存储结构。

ziplist 使用连续的存储空间，通过精心设计的存储格式有效节省存储空间。但是当元素个数比较多时，修改元素需要重新分配内存空间，影响 Redis 的执行效率，故而选择普通的双向链表。

quicklist 是什么？

quicklist 是 Redis 3.2 版本中新引入的数据结构，在时间和空间效率上实现了较好的折中。Redis 中对于 quicklist 的注释为 A doubly linked list of ziplists，即一个双向链表，每个链表节点都是一个 ziplist。

如下图所示，quicklist 结构中 head 和 tail 是指向首尾节点的指针，count 是 quicklist 中的元素总数（即所有 ziplist 元素个数之和），len 是 quicklist node 的个数，fill 用于指明每个节点中 ziplist 的长度（为正数时表示最多含有的数据项数，为负数时用于表示 ziplist 节点最大的大小，-1 到 -5 分别表示 4KB 到 64 KB）。

当 quicklist 中节点个数较多时，由于我们经常访问的是两端的数据，为了进一步节省空间，Redis 允许对中间的节点进行压缩，compress 参数用于指定两端各有 compress 个节点不压缩。

下面给出了 quicklist 中节点的大小及各数据项的含义：

typedef struct quicklistNode {
    struct quicklistNode *prev;
    struct quicklistNode *next;
    unsigned char *zl;
    unsigned int sz;             /* ziplist size in bytes */
    unsigned int count : 16;     /* count of items in ziplist */
    unsigned int encoding : 2;   /* RAW==1 or LZF==2 */
    unsigned int container : 2;  /* NONE==1 or ZIPLIST==2 */
    unsigned int recompress : 1; /* was this node previous compressed? */
    unsigned int attempted_compress : 1; /* node can't compress; too small */
    unsigned int extra : 10; /* more bits to steal for future usage */
} quicklistNode;

More about quicklist

quicklist 通常在每个节点中的 ziplist 最大大小为 8KB 时可以提供最佳性能，可以参考以下资料：

• https://matt.sh/redis-quicklist-visions
• https://matt.sh/redis-quicklist

listpack

为什么需要listpack？

Redis 作者提到原有的 ziplist 实现了很好的内存利用优化，同时支持双向遍历，但是在实际使用中除了级联更新外，还可能出现一些问题，因此进一步设计了 listpack 数据结构。

Redis 官方对于 listpack 的解释为 A lists of strings serialization format，即一个字符串列表的序列化格式。Redis 5.0 版本引入了 listpack，最初用做 Stream 类型的底层实现，直到 Redis 7.0 版本中才完全替代 ziplist。

listpack是什么？

下面给出了 listpack 的数据结构，主要由四部分组成，包括 6byte 的表头元数据，若干个列表节点以及最后的 1byte 的结束标识符。

| tot-bytes | num-elements | e1 | e2 | ... | eN | listpack-end-byte |

# 各部分说明
Total bytes：整个 listpack 的空间大小，占用 4 个字节
Num of elements：listpack 中的 entry 个数，占用 2 个字节。当 entry 个数大于等于 65535 时该元素设置为 65535，此时元素个数需要通过遍历得到
Entry：具体元素
End byte：listpack 结束标志，占用 1 个字节，内容为 0xFF。

每个 listpack 节点的内容如下，通过精心设计的 element len 字段保存每个 entry 自身的长度，支持前向和后向遍历，从而避免了节点更新时的连锁更新问题。

| encoding-type | element-data | element-tot-len |
    
# 各部分说明
encoding-type：元素的编码类型
element-data：实际存储的数据，可能为空，因为部分小的元素可以直接存储在 type 中
element-tot-len：encoding 和 data 的长度之和，占用字节数小于等于 5
    - element-tot-len 所占用的每个字节的第一个 bit 用于标识；0代表左侧已没有更多字节，1代表左侧还有字节，每个字节只有7 bit 有效。
    - element-tot-len 主要用于从后向前遍历，当需要找到当前元素的上一个元素时，可以从后向前依次查找每个字节，直至找到结束的字节确定上一个 entry 的长度。

TODO

• { } ziplist / quicklist / listpack 源码阅读
• { } ziplist / listpack 优缺点对比

参考资料

1. 《Redis设计与实现》Ch7
2. 《Redis 5设计与源码分析》
3. listpack官方介绍
4. 深入分析redis之listpack，取代ziplist?
5. 从ziplist到quicklist，再到listpack的启发
6. 【Redis】ziplist与listpack源码剖析：Redis数据存储的演进与优化

起因

我的服务器中部署了一个typecho博客和两个使用docker容器的服务，其中docker容器使用端口映射，将容器中的端口映射到宿主机上的端口实现访问。

一次偶然机会发现服务器上的服务可以通过IP+端口的方式直接访问，如果有未备案的域名解析到我们服务器的IP，可能会导致云服务器厂商关停我们的服务造成一些问题。因此，我们需要禁止通过IP+端口直接访问服务。

Nginx 配置

这里的三个服务通过nginx进行转发，对不同server_name的请求会直接转发到对应的服务进程。因此，这里有限考虑使用nginx配置来禁止IP+端口的访问。服务器上主要开放了两个端口，80和443，分别用于HTTP和HTTPS请求，在实际进行相应配置时二者也有所不同。

80 端口

对于80端口，我们在nginx.conf中添加如下配置。具体原理在于，当根据listen无法得到最佳匹配时，nginx会使用请求中的Host值匹配server_name，匹配顺序可以参考这篇博客。IP+端口进行请求时匹配到下面的server配置，直接返回403错误信息。

server {
    listen 80 default_server;
    server_name  _;    
    return 403;
}

443端口

由于使用了HTTPS协议，因此还需要禁止通过IP+443端口的访问方式。具体参考了下面的博客：

• https://www.huixiangdou.cn/archives/nginx-jin-zhi-80-443-duan-kou

具体来说，Nginx 上对于 SSL 服务器在不配置证书的时候会出现协议错误，哪怕端口上配置了其他网站也会报错。因此，我们需要随便生成一个证书进行配置，生成 SSL 证书可以使用这个网站https://myssl.com/create_test_cert.html。在nginx.conf中添加如下配置：

server {
    listen 80 default;
    listen 443 default_server;
    #SSL-START SSL相关配置，请勿删除或修改下一行带注释的404规则
    #error_page 404/404.html;
    ssl_certificate /path/to/cert.pem;
    ssl_certificate_key /path/to/private.key;
    ssl_protocols TLSv1 TLSv1.1 TLSv1.2;
    ssl_ciphers ECDHE-RSA-AES128-GCM-SHA256:ECDHE:ECDH:AES:HIGH:!NULL:!aNULL:!MD5:!ADH:!RC4:!DH:!DHE;
    ssl_prefer_server_ciphers on;
    ssl_session_cache shared:SSL:10m;
    ssl_session_timeout 10m;
    error_page 497  https://$host$request_uri;
    #SSL-END
    server_name _;
    return 403;
}

配置完成后重载 Nginx 配置。

$ nginx -t
$ nginx -s reload

Docker容器问题

Docker容器通过端口映射实现服务的对外可用性，这里是通过-p host_port:container_port实现容器上的端口到宿主机上端口的映射。具体来说，以容器的80端口映射到宿主机的8080端口为例，docker容器运行时使用了-p 8080:80，Nginx中监听了80端口，并在对应域名访问时将请求转发到服务器的8080端口。

location / {
    proxy_pass http://host_ip:8080;
}

但是，在根据上面的配置禁止了直接使用IP+80/443端口访问的方式后，发现host_ip:8080仍然能够访问到docker容器中的服务。查询相关资料修改了iptables路由表和sfw防火墙规则后，仍然无法解决问题。防火墙上没有打开端口，但仍然可以访问。最后通过查找资料发现是docker自身的原因，下面是docker官方的介绍：

If you don't specify an IP address (i.e., -p 80:80 instead of -p 127.0.0.1:80:80) when publishing a container's ports, Docker publishes the port on all interfaces (address 0.0.0.0) by default. These ports are externally accessible. This also applies if you configured UFW to block this specific port, as Docker manages its own iptables rules. Read more

大致意思是说docker容器中设置端口映射时如果没有指定宿主机IP，那么默认映射到0.0.0.0，即所有IP都可以访问。并且由于Docker镜像自行管理其路由表规则，设置宿主机防火墙也不起作用。知道原因后，我们只需要修稿docker容器的端口映射即可，对于正在运行的docker容器，修改方式参考如下博客，修改对应容器的/var/lib/docker/containers/{container_id}/hostconfig.json中的PostBindings->HostIp，HostIp设置为127.0.0.1即可。

• https://blog.csdn.net/km_bandits/article/details/135724252

参考资料

• Nginx配置禁止IP访问80和443端口
• Nginx禁止未绑定域名或IP访问80和443端口实践小结
• docker端口映射后,外部可以直接通过宿主机未开启的端口访问到服务的问题?
• docker修改已运行容器的映射端口

• https://programmercarl.com/0028.%E5%AE%9E%E7%8E%B0strStr.html

问题

给定一个字符串$s$(长度为N)和一个模式串$t$(长度为M)，如果$s$中存在$t$，那么返回模式串第一次出现的起始索引；如果不存在返回-1。对应Leetcode 28. 找出字符串中第一个匹配项的下标

KMP算法

KMP算法是由D.E.Knuth，J.H.Morris和V.R.Pratt同时发现的一种快速的字符串匹配算法，时间复杂度为$O(M+N)$。KMP算法的核心思想是在字符串匹配失败时利用之前已经匹配的信息来做快速回退，避免从头再做匹配。KMP算法的核心函数是一个用于求解next数组的函数，next数组包含了模式串局部匹配的信息。

这里代码随想录中给出了关于next数组的详细解释。next数组对应自定义的前缀表，其中前缀表是一个和模式串长度相同的数组，前缀表第i个位置的值为[0,i]子字符串的最长相同前后缀的长度；

• 前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串；
• 举例来说，“aab”的前缀有“a”和“aa”、后缀有“b”和“ab”，“aabaa”的最长相同前后缀长度为2，“aa”的最长相同前后缀长度为1。

以下图为例，假设文本串和模式串分别为aabaabaafa和aabaaf，前缀表如图中所示。那么在b和f不匹配时，此时寻找前缀表中前一位存储的值，查找得到值为2，该值的含义是“aabaa”的最长相同前后缀长度为2，即“aa”。此时我们可以不用从头开始重新匹配，文本串中的匹配指针可以不移动，将模式串中的匹配指针回退到索引2处重新开始匹配即可。

• 这里为什么可以不回退文本串的匹配指针？

  因为这里通过回退j指针，找到了从文本串中该位置向前的最长相同前后缀，获得了类似下图的效果。

• 实际使用中常通过将前缀表统一减1得到next数组，那么如何计算next数组？

  next数组的计算类似于移动模式串，在模式串和模式串之间做匹配，在移动的过程中计算next数组的值，next数组的计算代码如下所示：

  void getNext(int* next, const string& s){
    int j = -1;
    next[0] = j;
    for(int i = 1; i < s.size(); i++) { // 注意i从1开始
        while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
            j = next[j]; // 向前回退
        }
        if (s[i] == s[j + 1]) { // 找到相同的前后缀
            j++;
        }
        next[i] = j; // 将j（前缀的长度）赋给next[i]
    }
  }

• 基于next数组进行文本串和模式串的匹配代码如下：

  void match(string s, string t) {
    int j = -1;
    int next[t.size()];
    getNext(next, t);
  
    for (int i = 0; i < s.size(); i++) {
        while (j >= 0 && s[i] != t[j+1]) {
            j = next[j];
        }
        if (s[i] == s[j+1]) {
            j++;
        }
        if (j == (t.size() - 1)) {
          return i - t.size() + 1;
        }
    }
    return -1;
  }

站点迁移

之前使用的是云服务器是腾讯与的2核4G服务器，但是由于最开始购买时只买了一年，续费时价格太贵，因此转到阿里云，可以有四年每年99元的2核2G服务器可以白嫖~

迁移过程大概分为两步：站点数据迁移和站点备案迁移

数据迁移

博客迁移wordpress->typecho

原来的博客使用wordpress框架，但是wordpress框架功能齐全、有些臃肿，因此这里换成了更精简的typecho框架。

1. typecho安装
   参考了知乎博客https://zhuanlan.zhihu.com/p/34211709；

2. 导出wordpress数据库并在新服务器中导入

   • mysql导入导出命令参考: https://www.runoob.com/w3cnote/linux-mysql-import-export-data.html；
   • 先将原服务器上的wordpress数据库导出为*.sql文件，再导入到新服务器中；
   • 这一步是为了方便下一步转换到typecho，因为这样可以直接访问本地数据库。
3. 数据迁移到typecho
   基于typecho插件：https://docs.typecho.org/plugins/wordpress-to-typecho

4. 还原wordpress中的图片附件到typecho中

   • 将WordPress的wp-content/uploads目录下的附件全部移动到Typecho的usr/uploads目录下，保持目录结构不变。
   • 在mysql typecho对应数据库中执行以下代码以完成图片路径的替换：

    update typecho_contents set text=replace(text,'wp-content/uploads','usr/uploads')
    update typecho_contents set text=replace(text,'wordpree站点url','typecho站点url')

5. typecho使用数学公式
   使用插件：https://github.com/yuzhongzhibi/typecho_mathjax_plugin
6. typecho主题页面更改
   参考链接：https://www.skyqian.com/archives/typecho-pages.html
7. typecho使用redis cache加速访问
   参考链接：https://www.shuyz.com/posts/use-typecho-redis-cache-to-speedup-typecho-blog/
   这里是使用了一个 php 的 redis 客户端，每次修改页面内容时要刷新 redis 缓存，通过在请求链接后添加如下参数实现：
8. 清除页面缓存：?debug=true&userkey=&action=purgepage
9. 清除整站缓存：?debug=true&userkey=&action=purgeall

docker容器迁移

做法是现在新服务器上安装docker，然后迁移旧服务器上的docker挂载文件夹到新服务器相同位置，最后在新服务器启动容器。参考链接：https://zhuanlan.zhihu.com/p/643367054
这里我主要使用了两个容器用于存储电子书和笔记

1. Talebook：https://github.com/talebook/talebook
2. leanote: https://www.bilibili.com/read/cv23693842/

站点备案迁移

为了方便使用，计划将域名和服务器都转移到阿里云。因为服务器需要在所在服务商处备案，因此还需要在阿里云备案，主要参考了这篇博客：https://www.zuozuovera.com/posts/1644/。

差分数组

• 参考教程：https://wansuanfa.com/index.php/589
• leetcode题目：1109. 航班预订统计

问题描述

给定一个数组，需要频繁地对某个区间内的元素做加减操作，并获取最后的操作结果。常规做法是每次都遍历整个区间然后修改区间内的元素，但是元素的访问需要时间、频繁访问元素会减慢程序的运行时间。因此，可以使用差分数组来进行优化。

一维差分数组定义

一维差分数组$ d[n] $定义为原始数组$ nums $相邻元素之间的差，即$d[i]=nums[i]-nums[i-1]$，其中$d[0]=nums[0]$。这样原数组就是差分数组的前缀和

$$ nums[i] = \sum_{k=0}^i d[k]. $$

由此，我们可以改进原来的区间操作，如对区间$[a,b]$内每个元素加3，那么只需要在区间的两端进行操作即可，即

$$ d[a] += 3, d[b+1] -= 3 $$

证明

假设$nums1$是修改后的数组，$d1$是修改后的差分数组，其中$d1[a]=d[a]+3, d1[b+1]=d[b+1]-3$.

• 对于$0\leq i \lt a$, $nums1[i] = \sum_{k=0}^i d1[k] = \sum_{k=0}^i d[k] = nums[i]$.

• 对于$a\leq i \leq b$,

  $$ \begin{align} nums1[i] &= \sum_{k=0}^i d1[k] \\&= \sum_{k=0}^{a-1}d[k] + \sum_{k=a+1}^{b}d[k] + d[a] + 3 \\&= \sum_{k=0}^i d[k] + 3 \\&= nums[i]+3 \end{align}. $$

• 对于$i \gt b$,

  $$ \begin{align} nums1[i] &= \sum_{k=0}^i d1[k]\\ &= \sum_{k=0}^{a-1}d[k] + \sum_{k=a+1}^{b}d[k] + \sum_{k=b+1}^{i}d[k] + d[a] + 3 + d[b] - 3\\ &= \sum_{k=0}^i d[k] + 3 - 3\\ &= nums[i]. \end{align} $$

  由此，可以证明只修改差分数组的两端即可以修改原数组的整个区间。

代码

class Solution {
public:
    vector<int> diff;
    vector<int> nums;

    void diffNums() {
        diff[0] = nums[0];
        for(int i = 1; i < nums.size(); ++i) {
            diff[i] = nums[i] - nums[i-1];
        }
    }

    void increment(int a, int b, int val) {
        diff[a] += val;
        if (b + 1 < diff.size())
            diff[b + 1] -= val;
    }

    void result() {
        nums[0] = diff[0];
        for (int i = 1; i < diff.size(); i++)
            nums[i] = diff[i] + nums[i - 1];
    }

    vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
        nums.resize(n, 0);
        diff.resize(n, 0);
        diffNums();
        for (int i = 0; i < bookings.size(); ++i) {
            increment(bookings[i][0]-1, bookings[i][1]-1, bookings[i][2]);
        }
        result();
        return nums;
    }
};

拓展 - 二维差分数组

二维差分数组可以在一维差分数组的基础上进行拓展，视为一个平面，定义如下

$$ d[i][j] = nums[i][j] - nums[i-1][j] - nums[i][j-1] + nums[i-1][j-1] $$

那么相应地

$$ nums[i][j] = nums[i-1][j] + nums[i][j-1] - nums[i-1][j-1] + d[i][j] $$

假设以 $(x1,y1)$ 为左上角， $(x2,y2)$ 为右下角构成一个区间$S$，如果对这个区间内的每个元素增加$val$，只需要执行下面四步即可。

$$ \begin{align} &d[x1][y1] += val \\ &d[x1][y2+1] -= val \\ &d[x2+1][y1] -= val \\ &d[x2+1][y2+1] += val \end{align} $$

证明

同样假设$num1$和$d1$是修改后的数组和查分数组，以下分情况进行讨论

• 对于$(m,n)$满足$m<x1$或$n<y1$, 容易知道该范围内查分数组未发生变化，求解该范围内的数组不需要用到区间$S$内的差分数组，因此该范围内数组不受影响；

• 对于$(m,n)\in S$, 不妨设原数组$num$的元素均为$a$, 那么

  $$ \begin{align} nums1[x1][y1] &= nums1[x1-1][y1] + nums1[x1][y1-1] - nums1[x1-1][y1-1] + d1[x1][y1]\\ &= nums[x1-1][y1] + nums[x1][y1-1] - nums[x1-1][y1-1] + d[x1][y1] + val\\ &= nums[x1][y1] + val; \end{align} $$

  对于$S$内的其他点，使用此递推公式同样可以推导出

  $$ nums1[m,n] = nums[m][n]+val $$

• 对于$(m,n)$满足$x1\leq m \leq x2$且$n\gt y2$, 我们可以知道

  $$ \begin{align} nums1[x1][y2+1] &= nums1[x1-1][y2+1] + nums1[x1][y2] - nums1[x1-1][y2] + d1[x1][y2+1]\\ &= nums[x1-1][y2+1] + nums[x1][y2] + val - nums[x1-1][y2] + d[x1][y2+1] - val\\ &= nums[x1][y2+1]; \end{align} $$

  对于其他$(m,n)$使用递推公式同样可以发现数组的值没有发生变化。

• 对于$(m,n)$满足$m\gt x2$且$y1\leq n \leq y2$, 可以使用类似上一种情况的方式推导发现数组数值未发生变化；

• 最后，对于$(m,n)$满足$m\gt x2$且$n\gt y2$，我们考虑

  $$ \begin{align} nums1[x2+1][y2+1] &= nums1[x2][y2+1] + nums1[x2+1][y2] - nums1[x2][y2] + d1[x2+1][y2+1]\\ &= nums[x2][y2+1] + nums[x2+1][y2] - nums[x2][y2] - val + d[x2+1][y2+1] + val\\ &= nums[x2+1][y2+1]; \end{align} $$

  对于该区域其他点可以类推。

由此，我们得到，差分数组定义以及更新方式满足条件。

代码（来自参考链接）

// Java代码，需要注意边界情况
private int[][] d;// 差分数组。
private int[][] a;// 原数组。

public TwoDiffNums(int[][] a) {
    this.a = a;
    int m = a.length;
    int n = a[0].length;
    d = new int[m][n];
    // 求差分数组。
    for (int i = 0; i < m; i++)
        for (int j = 0; j < n; j++)
            add(i, j, i, j, a[i][j]);
}

public void add(int x1, int y1, int x2, int y2, int val) {
    d[x1][y1] += val;
    if (y2 + 1 < d[0].length)
        d[x1][y2 + 1] -= val;
    if (x2 + 1 < d.length)
        d[x2 + 1][y1] -= val;
    if (x2 + 1 < d.length && y2 + 1 < d[0].length)
        d[x2 + 1][y2 + 1] += val;
}

// 返回结果数组。
public int[][] result() {
    for (int i = 0; i < a.length; i++) {
        for (int j = 0; j < a[0].length; j++) {
            int x1 = i > 0 ? a[i - 1][j] : 0;
            int x2 = j > 0 ? a[i][j - 1] : 0;
            int x3 = i > 0 && j > 0 ? a[i - 1][j - 1] : 0;
            a[i][j] = x1 + x2 - x3 + d[i][j];
        }
    }
    return a;
}

LeetCode题目链接

二叉树的前序遍历：https://leetcode.cn/problems/binary-tree-preorder-traversal/
二叉树的中序遍历：https://leetcode.cn/problems/binary-tree-inorder-traversal/
二叉树的后序遍历：https://leetcode.cn/problems/binary-tree-postorder-traversal/

二叉树的遍历方法有两种，分别是递归法和迭代法；实际使用中由于系统调用栈有限制，使用递归法可能会导致栈溢出，这里记录三种遍历的迭代做法。最后，介绍二叉树层序遍历的两种方法。

迭代遍历法借助辅助栈实现，下面是二叉树节点的定义，使用链表实现。

 struct TreeNode {
     int val;
     TreeNode *left;
     TreeNode *right;
     TreeNode() : val(0), left(nullptr), right(nullptr) {}
     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 };

前序遍历

前序遍历的顺序是中左右，每次先处理中间节点，那么先将根节点入栈，然后将右孩子入栈，再将左孩子入栈。先右后左的原因是因为入栈顺序和处理顺序是相反的。前序遍历的处理代码如下：

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> st;
        if (root == NULL) {
            return res;
        }

        st.push(root);
        while (!st.empty()) {
            TreeNode *cur = st.top();
            st.pop();
            res.push_back(cur->val);
            if (cur->right) st.push(cur->right);
            if (cur->left) st.push(cur->left);
        }

        return res;
    }
};

中序遍历

中序遍历处理顺序为左中右，先访问二叉树顶部的节点，随后逐层向下访问直到树最左侧的节点，再开始处理节点，这导致处理节点的顺序和访问节点的顺序不一致。中序遍历的迭代法如下所示：

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> st;
        if (root == NULL) {
            return res;
        }
        TreeNode *cur = root;
        while (cur!=NULL || !st.empty()) {
            if (cur != NULL) {
                if (cur) st.push(cur);
                cur = cur->left;
            } else {
                cur = st.top();
                st.pop();
                res.push_back(cur->val);
                cur = cur->right;
            }
        }
        return res;
    }
};

后序遍历

先序遍历是中左右，后续遍历是左右中，那么只需要调整一下先序遍历的代码顺序，就变成中右左的遍历顺序，然后在反转result数组，输出的结果顺序就是左右中了。后序遍历的代码如下所示：

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> st;
        if (root == NULL) {
            return res;
        }
        st.push(root);
        while (!st.empty()) {
            TreeNode *cur = st.top();
            st.pop();
            if (cur->left) st.push(cur->left);
            if (cur->right) st.push(cur->right);
            res.push_back(cur->val);
        }
        reverse(res.begin(), res.end());
        return res;   
    }
};

统一的迭代遍历法

参考https://programmercarl.com/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E7%BB%9F%E4%B8%80%E8%BF%AD%E4%BB%A3%E6%B3%95.html
每次在待处理节点入栈后，加入一个NULL节点作为标记，之后在遇到NULL节点时处理栈中的下一个节点。需要注意的是，这种方法效率不高，节点可能会多次入栈。

层序遍历

// 迭代遍历，BFS基于队列
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> res;
        queue<TreeNode*> q;
        if (root == NULL)  {
            return res;
        }

        q.push(root);
        while (!q.empty()) {
            int size =q.size();
            vector<int> layer;
            for (int i = 0; i < size; ++i) {
                TreeNode *cur = q.front();
                q.pop();
                layer.push_back(cur->val);
                if (cur->left) q.push(cur->left);
                if (cur->right) q.push(cur->right);
            }
            res.push_back(layer);
        }
        return res;
    }
};

// 递归，DFS
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> res;
        queue<TreeNode*> q;
        if (root == NULL)  {
            return res;
        }

        order(0, root, res);
        return res;
    }

    // DFS, 递归
    void order(int depth, TreeNode *cur, vector<vector<int>> &res) {
        if (cur == NULL) return;
        if (res.size() == depth) res.push_back(vector<int>());
        res[depth].push_back(cur->val);
        order(depth + 1, cur->left, res);
        order(depth + 1, cur->right, res);
    }
};

leetcode题目链接：https://leetcode.cn/problems/sliding-window-maximum/

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值 。

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：

滑动窗口的位置	最大值
[1 3 -1] -3 5 3 6 7	3
1 [3 -1 -3] 5 3 6 7	3
1 3 [-1 -3 5] 3 6 7	5
1 3 -1 [-3 5 3] 6 7	5
1 3 -1 -3 [5 3 6] 7	6
1 3 -1 -3 5 [3 6 7]	7

示例 2：

输入：nums = [1], k = 1 输出：[1]

方法1：单调队列法

使用一个数据结构，每次滑动窗口时添加一个元素，删除一个元素，同时可以从队列头部获取想要的当前窗口内的最大值。这种数据结构就是单调队列，单调队列的pop和push操作应该遵循以下原则：

1. pop(value)：如果窗口移除的元素value等于单调队列的出口元素，那么弹出元素，否则不需要任何操作；
2. push(value)：如果push的元素value大于入口元素的值，那么将队列入口的元素弹出，直到push元素的数值小于等于队列入口元素的数值为止。
   基于如上规则，每次窗口移动后，队列头部元素就是当前窗口的最大值。

class MyQueue { //单调队列（从大到小）
public:
    deque<int> que; // 使用deque来实现单调队列
    // 每次弹出的时候，比较当前要弹出的数值是否等于队列出口元素的数值，如果相等则弹出。
    // 同时pop之前判断队列当前是否为空。
    void pop(int value) {
        if (!que.empty() && value == que.front()) {
            que.pop_front();
        }
    }
    // 如果push的数值大于入口元素的数值，那么就将队列后端的数值弹出，直到push的数值小于等于队列入口元素的数值为止。
    // 这样就保持了队列里的数值是单调从大到小的了。
    void push(int value) {
        while (!que.empty() && value > que.back()) {
            que.pop_back();
        }
        que.push_back(value);

    }
    // 查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
    int front() {
        return que.front();
    }
};

方法2：优先级队列

使用大顶堆，每次移动窗口时，将新的元素加入堆中，此时需要移除堆中不在窗口内的元素。为了记录堆中元素是否在窗口中，需要记录堆中元素在数组中的索引。在每次获取当前窗口内最大值之前，将堆顶的索引不在当前窗口内的元素移除。具体的实现方式如下：

class Solution {
    struct Node {
        int num;
        int idx;
        Node(int n, int i) : num(n), idx(i) {}
        bool operator < (const Node& b) const {
            return this->num != b.num ? (this->num < b.num) : (this->idx < b.idx);
        }
    };
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        priority_queue<Node> pq;
        vector<int> res;
        for (int i = 0; i < nums.size(); ++i) {
            pq.push(Node(nums[i], i));
            if (i >= k-1) {
                while (pq.top().idx <= i - k) {
                    pq.pop();
                }
                res.push_back(pq.top().num);
            }
        }
        return res;
    }
};

LJSon

• A C++ library for json parse/creation/update
• package地址：https://github.com/lishengxie/LJson

开发原因

最近在复习C++相关的知识，想要通过一个项目来巩固C++和算法的一些相关知识，但是网上推荐的相关C++项目大多比较复杂，很难下手。刚好最近实验室项目中频繁使用json文件，想到是否可以使用C++来实现一个json的解析库，在github上搜索后看到了一些现有的json仓库，初步了解后开始进行实现。

参考仓库

• https://github.com/510850111/cJSON/tree/master，在这个项目中学习了json对象的表示以及如何操作json对象；
• https://github.com/ACking-you/MyUtil/tree/master/json-parser，在这个项目中学习了如何从json字符串中解析数据，服用了部分解析json字符串的代码；
• https://github.com/nlohmann/json，著名的json处理库，从中学习了如何使用初始化列表来实现类Python的方式创建和更新json对象。

json文件格式

这里只做简单介绍，具体的格式可以参考json官网http://www.json.org。

json主要基于两种结构，分别是“键值对集合”和“值的有序列表”，前者可以看做字典或哈希表，后者可以看做数组。
1. 对象是无序的键值对集合，一个对象被包含在{}中，每个键值对的格式为key:value，其中key是字符串，value可以是字符串、布尔类型(true/false)、null、数值(整数或浮点数)、对象、数组；键值对之间使用,分隔，对象应该使用key索引对应的值；
2. 数组是值的有序集合，包含在[]中，值可以是前面提到的字符串、布尔类型(true/false)、null、数值(整数或浮点数)、对象、数组，值之间使用,分隔；

通过使用对象、数组以及支持两者之间的嵌套，json可以支持复杂的数据格式定义和传递。

使用数据结构表示json对象

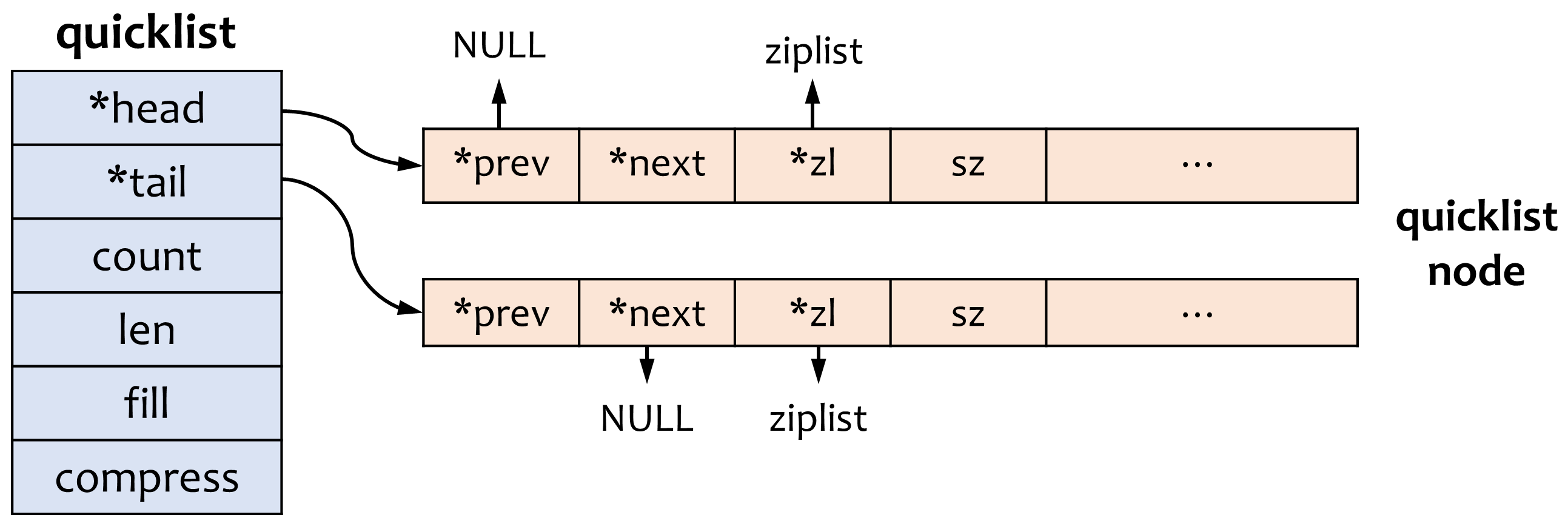
前面提到了json文件的格式，一种很自然的表示json对象的方式应该是使用字典表示对象，字典的值本身也可以是一个json对象，有一些json解析库中使用了这种方式，可以参考Python中json库对json文件的读写。我们使用了另外一种方式，即使用树形结构来表示整个json对象，如下图所示：

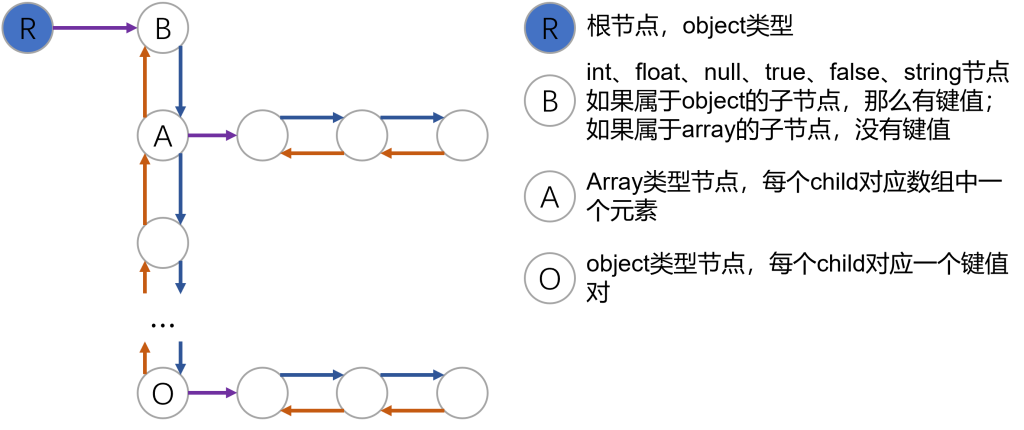
对应的C++定义如下，对象中的每个键值对以及数组中的每个值都使用一个JsonObject对象来表示，整个对象/数组的键值对/值使用双向链表进行表示，遍历整个双向链表即可以遍历整个json对象或数组。

enum JsonType {
    T_FALSE=0, T_TRUE, T_NULL, T_INT, T_FLOAT, T_STRING, T_ARRAY, T_OBJECT
};

class JsonObject {
    /* next和prev分别指向前一个对象和后一个对象 */
    JsonObject *next, *prev;
    /* Object和Array类型对象需要设置child指针 */
    JsonObject *child;
    /* Object的类型 */
    JsonType type;
    /* String对象的值 */
    char *valueString;
    /* 整数对象的值 */
    int valueInt;
    /* 浮点数的值 */
    double valueDouble;
    /* 键值对的键 */
    char *key;
}

以上图为例，假设有如下的json对象

{
    "name":"runoob",
    "alexa":10000,
    "sites": {
        "site1":"www.runoob.com",
        "site2":"m.runoob.com",
        "site3":"c.runoob.com"
    },
    "search":[ "Google", "Runoob", "Taobao" ]
}

那么对应到上面的树形结构应该为(以下提到的变量都是JsonObject类型)，首先有一个root表示整个json对象，root->child对应对象内键值对的双向链表，root->child对应"name":"runoob"，root->child->next对应"alexa":10000，以此类推。对于双向链表中的第四个节点node4，节点类型为数组，node4->child对应数组内值的双向链表，node4->child为"Google"，node4->child->next为Runoob，以此类推。第三个节点的对象也使用类似的方式表示。

方法设计

根据以上的数据结构，我们可以表示整个json对象，那么接下来就是对整个json对象的操作，应该包含两部分：

1. 从外部字符串解析出json数据对象；
2. 创建json对象并导出。

对于json对象，这里又进一步划分为了“增、删、改、查”四个部分，接下来分别对这四个部分的设计做一下介绍。

解析Json对象

这里参考了https://github.com/ACking-you/MyUtil/tree/master/json-parser中的解析方式，大致的实现思路为跳过给定字符串中的空白字符和注释，每次对于不同的字符解析出对应的对象。这里使用了C++标准库string中解析整数和浮点数的方法。

JsonObject* JsonParser::parse() {
    char token = get_next_token();

    if (token == 'n') {
        return parseNULL();
    }
    if (token == 't' || token == 'f') {
        return parseBool();
    }
    if (token == '-' || std::isdigit(token)) {
        return parseNumber();
    }
    if (token == '\"') {
        return parseString();
    }
    if (token == '[') {
        return parseArray();
    }
    if (token == '{') {
        return parseObject();
    }

    throw std::logic_error("unexpected character in parsing json.");
}

添加json节点

添加json节点应该是将给定的json节点添加到一个对象或数组中，对于添加到对象中，还需要同时提供键值对的key。添加的方法比较简单，在当前调用的JsonObject的child对应的双向链表中将给定的JsonObject对象插入，对于插入到对象中的情况还需要设置key。这里使用尾插法，即将新加入的节点插入到双向链表的尾部，方便检索。插入对象的实现方式如下所示，插入数组的实现类似。

void JsonObject::addItem(const char* iKey, JsonObject* item) {
    if(item == nullptr){
        return;
    }
    if (this->type != T_OBJECT) {
        throw std::logic_error("must be json object to add key-value pair");
    }

    // set key for item
    char* out = new char[strlen(iKey) + 1];
    strcpy(out, iKey);
    item->key = out;

    // no child yet
    if (this->child == nullptr) {
        this->child = item;
    } else {
        // 尾插法, 检索更快
        JsonObject* pChild = this->child;
        while (pChild!= nullptr && pChild->next!=nullptr){
            pChild = pChild->next;
        }

        pChild->next = item;
        item->prev = pChild;
    }
}

删除json节点

删除节点和增加节点相反，给定key从对应的对象中或给定index从给定的数组中删除对应的节点，同样是在数组中删除相应的节点，需要注意的是对于删除的节点需要及时释放相应的内存。释放内存被实现成了JsonObject类的静态方法，通过递归的方式释放，如下所示：

void JsonObject::deleteNode(JsonObject *node) {
    JsonObject *nextNode;
    JsonObject *curNode = node;
    while (curNode != nullptr) {
        nextNode = curNode->next;
        if (curNode->child) {
            deleteNode(curNode->child);
        }
        if (curNode->valueString) {
            delete [](curNode->valueString);
            curNode->valueString = nullptr;
        }
        if (curNode->key) {
            delete [](curNode->key);
            curNode->key = nullptr;
        }
        delete curNode;
        curNode = nextNode;
    }
}

查找json节点

给定key从对应的对象中或给定index从给定的数组中查找对应的节点，这里通过重载[]运算符实现，下面给出了给定key查找出对应值的实现，在key不存在的情况下会创建出一个null对象并返回。对于给定index查找数组的实现，在index超出数组索引范围的情况下会返回一个全局的查找标志表示返回失败，后续可以实现为添加对应数量的null节点。

JsonObject& JsonObject::operator[] (const char* iKey) {
    JsonObject *cur = this->child;
    while (cur != nullptr) {
        if(strcmp(iKey, cur->key) == 0) {
            return *cur;
        }
        cur = cur->next;
    }
    JsonObject *object = JsonObject::createNULL();
    this->addItem(iKey, object);
    return *object;
}

更改json节点

对于修改json节点，通过重载=运算符的方式加以实现，前面几个函数对数字、字符串、布尔值和空值几种基本数据类型实现了重载，最后一个函数提供通过initializer_list的方式来更新JsonObject。

JsonObject& operator=(int number);
JsonObject& operator=(double number);
JsonObject& operator=(const char* strValue);
JsonObject& operator=(bool boolValue);
JsonObject& operator=(std::nullptr_t nullValue);
JsonObject& operator=(std::initializer_list<InitType> initList);

对于前几个函数，实现的方式为修改节点的类型，如果被修改的节点是对象或数组类型，那么使用deleteNode方法删除其child指向的双向链表，以赋值为整数为例，其函数实现如下所示：

JsonObject& JsonObject::operator=(int number) {
    if (*this == LJson::npos) {
        std::cerr << "can not assign to non-existent object\n";
        return *this;
    }
    if (this->type == T_OBJECT || this->type == T_ARRAY) {
        JsonObject::deleteNode(this->child);
        this->child = nullptr;
    }
    this->type = T_INT;
    this->valueInt = number;
    return *this;
}

对于使用initializer_list来更新JsonObject的例子，通过自定义一个InitType结构体来加以支持，InitType会将初始化列表转换成一个数组类型的JsonObject，随后我们检查整个数组并进行数组到对象的转换。判断一个数组是否是对象的标准如下：
1. 数组中的每个值都是一个数组；
2. 数组中每个值对应的子数组长度都为2；
3. 数组中每个值对应的子数组的第一个元素都是字符串类型。

满足以上三个条件的数组应该被转换成一个对象，转换过程递归进行，具体实现可以参考github中的代码。

其他工具函数

提供了一个JsonParser工具类用于解析json字符串，提供了一个Json类来将JsonObject和JsonParser的功能进行封装，方便使用。此外，还提供了json对象转换为字符串的格式化方法。

待实现

• [ ] 检查实现中的动态内存分配和释放，避免造成内存泄漏；
• [ ] 有一些冗余代码，后续考虑使用模版函数进行替换；
• [ ] 接口目前有些混乱，另外异常情况目前没有很好地处理；
• [ ] 添加HashTable用于记录键->JsonObject指针，避免每次检索时都需要遍历，提高检索速度。

程序运行环境配置

C++

针对C++程序，重新下载代码编译；

Python

重新配置Python环境主要经历了以下步骤：
1. 下载miniconda安装程序并安装；
2. WSL2环境迁移到服务器中，这里选择直接打包WSL2下面的虚拟环境目录并到服务器相应目录下解压，参考了教程https://blog.csdn.net/qq_45893319/article/details/122226053;
3. 直接打包的环境，无法使用pip的问题，可以通过修改pip文件解决，参考教程https://blog.csdn.net/qq_40933913/article/details/127907916
4. 环境迁移后发现在迁移的环境中无法使用clear命令，原因是迁移过来的环境中clear文件有问题。解决方案如下：

• 在出错的环境下，输入which clear，然后将clear地址重命名，下次再clear时会生成新的。
  
  
  

  mv /home/xxx/.conda/envs/yolox/bin/clear /home/xxx/.conda/envs/yolox/bin/clear_old
  

vscode连接服务器开发

参考教程https://blog.csdn.net/ffriend/article/details/126680223。
由于服务器离线，使用vscode连接时无法在远程服务器上下载vscode-server，这里需要手动下载一下。步骤如下
1. 查看本地vscode的commit id：帮助-关于，复制commit id
2. 本地下载vscode-server

wget https://update.code.visualstudio.com/commit:${commit_id}/server-linux-x64/stable
# 注意把:${commit_id}替换成对应的Commit ID

3. 复制到服务器并安装

rm ~/.vscode-server/bin/* -rf  #把$HOME/.vscode-server/bin下的内容删干净，防止出错
cd ~/.vscode-server/bin
tar -zxf vscode-server-linux-x64.tar.gz
mv vscode-server-linux-x64 ${commit_id} # 注意把:${commit_id}替换成对应的Commit ID

服务器安装screen应用

参考教程https://blog.csdn.net/Demo_Null/article/details/110873673，主要是编译安装screen和ncurses两个可执行程序，这里需要管理员权限，负责无法安装到默认的安装位置。

screen常用命令如下

1、启动共享窗口：screen -S 名称
2、查看当前所有共享会话：screen -ls
3、进入共享会话：screen -r 名称
4、退出共享会话：ctrl +a +d

NoC仿真器

NoC(Network on chip)是连接同构或者异构多核心的重要的系统互联结构，NoC仿真器提供了对NoC中多种性能指标的仿真。下面这篇博客中列出了常用的开源NoC仿真器，https://networkonchip.wordpress.com/2011/02/22/simulators/ ，目前了解到最常用的两种分别是

1. noxim，基于SystemC语言开发，修改和添加新功能较为灵活。

   • 开源地址：https://github.com/davidepatti/noxim

2. booksim，基于C++语言开发，是 Principles and Practices of Interconnection Networks 这本书的配套教程。

   • 开源地址：https://github.com/booksim/booksim，https://github.com/booksim/booksim2

SNN仿真器

SNN是第三代人工神经网络，基于脉冲传递数据和信息，由于SNN本身具有稀疏性（连接稀疏性和脉冲稀疏性），因此有许多神经形态硬件（Loihi、SpiNNaker、TianjiC、Darwin等）被开发出来用于SNN加速。这里主要列出一些在通用的CPU和GPU平台上进行SNN加速的一些SNN仿真器。

1. NEST，可以用于SNN网络信息处理，网络活动动态、学习和突触可塑性等

   • 开源地址：https://github.com/nest/nest-simulator/

2. Brain2，时钟驱动的SNN仿真器

   • 开源地址：https://github.com/brian-team/brian2

3. GeNN，GPU加速的SNN仿真器

   • 开源地址：https://github.com/genn-team/genn

4. Carlsim，GPU加速的SNN仿真器

   • 开源地址：https://github.com/UCI-CARL/CARLsim6

5. Auryn，RSNN仿真器

   • 开源地址：https://github.com/fzenke/auryn

6. ANNarchy

   • 开源地址：https://github.com/ANNarchy/ANNarchy

7. Spike， GPU加速的SNN仿真器

   • 开源地址：https://github.com/nasiryahm/Spike

8. Spice，多GPU、时钟驱动的SNN仿真器

   • 开源地址：https://github.com/denniskb/spice

9. Nengo，基于Python的神经网络仿真

   • 开源地址：https://github.com/nengo/nengo

10. Brain2Loihi，基于brain2实现的Loihi模拟器

    • 开源地址：https://github.com/sagacitysite/brian2_loihi

11. NeuroSync

    • 开源地址：https://github.com/SNU-HPCS/NeuroSync

12. dynapse-simulator，Dynap-SE1神经形态硬件仿真器

    • 开源地址：https://github.com/YigitDemirag/dynapse-simulator
13. 待添加